Advantage diminishing

How important is comparative advantage in determining the marginal value of additional population?

Comparative advantage is the principal in economics that explains why all countries benefit from trade, rather than merely those that are most efficient at producing given goods and services. If Britain can produce 20 cars or 40 computers, and the United States 100 cars or 500 computers, total production could be 60 cars and 270 computers in the absence of exchange but 65 cars and 275 computers with free trade, were Britain to shift to only producing cars. For our purposes, what matters is that the same method can be applied to trade between individuals as well as between countries. Previously this blog has modelled the technological externalities from one additional individual, and found them to be extremely substantial under all reasonable discount rates: in this post, whether comparative advantage externalities are also substantial will be explored.

Figure 1: A production possibility frontier in goods X and Y. Points A and B are possible and Pareto optimal: point C is possible and not Pareto optimal: point D is impossible.

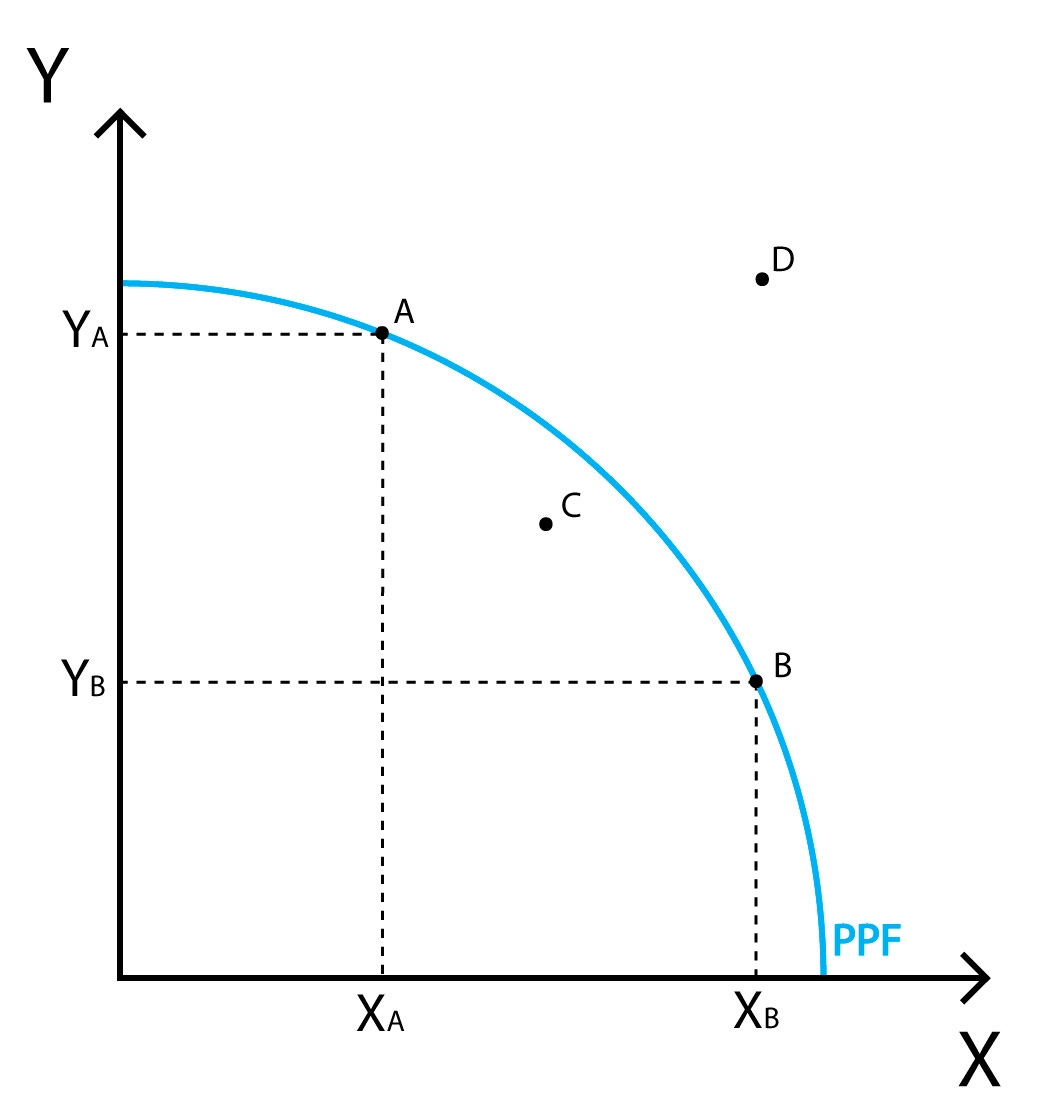
Comparative advantage can be visualised on a production possibility frontier (PPF) such as Figure 1. This represents the ability of society to produce two consumer goods X and Y, and any point along the PPF is Pareto Optimal - production of one good can only be increased by decreasing that of another - while only a single point is allocatively efficient - the optimal ratio of each good to produce. If consumers utility functions are log in all goods differing by constants, then all individuals will buy the same ratio of X and Y as society does. Let X’ and Y’ represent the maximum possible production of X and Y respectively.

Diminishing marginal returns to all inputs mean that the worst possible structure to the diagram would be a straight line from X’ to Y’, and the best possible a square with X’ and Y’ as vertices. Comparative advantage as opposed to specialisation, scale or innovation is unable to increase X’ and Y’, but merely able to increase the ability of society to realise consumption levels of X and Y where both have substantial value. This, in a manner unlike innovation, thus necessarily caps the per-capita benefit - no gain beyond a doubling in consumption of all goods can occur from comparative advantage alone.

Figure 2: Production possibility frontiers under populations of 10, 100, 1000, 10000 and 100000.

Figure 3: Production per capita of each good relative to maximum possible production of either good, by population level.

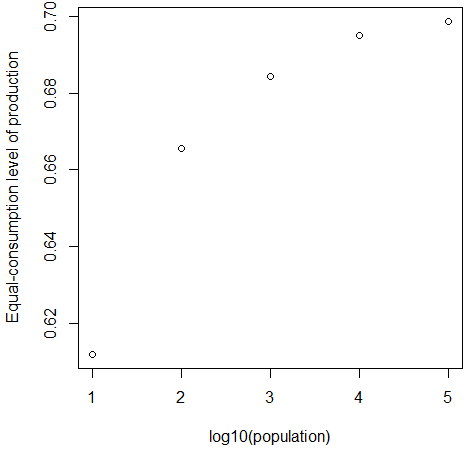
The results from using individual ability distributions under a Pareto distribution with a value for alpha of 1.75 are shown above. As can be seen, the space for gains is limited, and the gains from even very large proportional increases in the population become very small, with the gain from even moving from a population of 10,000 to 100,000 representing but 0.6% of total production in that year at most, in the case where the goods should be produced in constant proportions. The benefits from higher population in the effects on technology and public goods provision remain substantial: additionally, by allowing more firms to access the minimum efficient scale, the promotion of competition - but comparative advantage is far less important.

This suggests that comparative advantage effects are near-insignificant when determining optimal populations in the two-good case. However, the economy of the real world contains more than two goods, and in cases with larger numbers of goods the effects could remain substantial even at current levels of population due to the higher degrees of freedom. Additionally, free trade does not only bring benefits due to comparative advantage but due to the accessibility of increased returns to scale, which are entirely absent in the above model. Quantifying these effects will be done in a future post.