Innovative externality inclusion
If the current level of regulation is privately optimal, how does inclusion of innovation externalities change the optimal global level?
Over the past hundred years, the total amount of regulation on activity in the economy has increased dramatically across the developed world. This may have brought counterfactual benefits, such cleaner water, safer consumer goods and greater privacy, at the expense of costs such as sluggish bureaucracies, lowered business formation rates and slower development of new products. All of these effects share the key trait of being mostly internalised - citizens of the country that implements the regulations bear and receive about 100% of the costs and benefits. However, a key negative effect of regulation, namely the reduction in innovation, affects all countries around the world due to technological discovery being a public good in the long run - not just the country which implemented the regulation. This post determines the change in the optimal level of regulation that results if foreign welfare is viewed as equally valuable to native upon accounting for the effects of technological change.
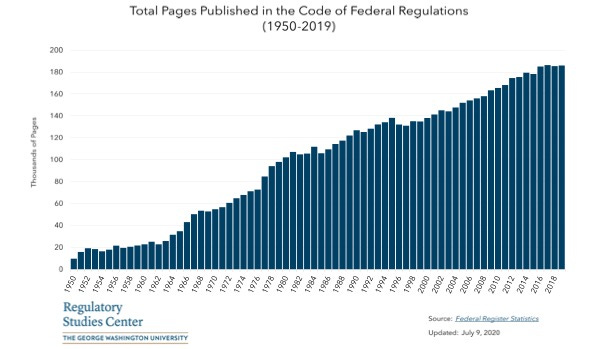
For the purposes of this post, the dataset that will be used is the Code of Federal Regulations, which has the advantage of running continuously since 1949 (with annual supplements listing changes published from 1938 to 1949). It is also the focus of the academic literature that is relevant to our purposes by estimating the effect of regulatory changes of countries on the productivity frontier. It likely represents a decent proxy for regulation as longer regulatory codes should be expected to be more burdensome to comply with, and thus bring greater costs.
Several studies make estimates relevant to our purposes of the effects of regulation on economic growth. Dawson and Seater 2013 adapt a model of taxation’s impacts on the economy to measure the effects of the increase in regulation from 1949 to 2005, although difficulties in classification and measurement mean that they neither differentiate regulations by type nor include the effects of state-level regulations. They find that regulation has effects on the trend level of output, but some of these are lagged, with the result that they measure a net reduction in trend output growth of 1.9% over the period while the average long-run effect is a reduction in 2.2%. Loayza et al 2005 find that a one-standard-deviation increase in regulation reduced GDP growth per year by 0.4%, which given the 500% increase in the regulatory level above is equivalent to a 2.4% reduction in the annual growth rate. Bourles et al 2013 find the aggregate effect of all regulation to be a reduction of annual growth of 1%: however, this may be of more limited use than the above studies as under a model whereby the regulations with the positive or least deleterious effects on economic growth are implemented first this does not provide an estimate of the marginal effect. However, it has the advantage of finding that the costs of regulation increase the closer to the technological frontier a country is, implying that the results are primarily due to suppressing innovation rather than one-off growth boosts. Due to concerns with the possible one-off nature of gains, this blog will use the average of Bourles et al 2013 and half of each of Loayza et al 2005 and Dawson and Seater 2013 of 1.1%.
Importantly, it must be stressed before any further discussion that even very small effects on trend growth rates have titanic welfare implications - Robert Lucas argued that once you start thinking about economic growth it is hard to think about anything else1. A 2% difference in growth rates multiplies per capita incomes by a factor of 7.2 if maintained over a century: undoing growth in Britain by this factor would reduce incomes to the level they were at slightly before the formation of Germany. As utility is natural log of consumption in economics, the entire increase in living standards from the days of 5 year old chimney sweepers to today would be replicated by such a change.
Before it is possible to determine the impact on the optimal aggregate quality of regulation, two further factors need quantifying: the lag between innovation in one country and implementation of the technology in another, and the discount rate to determine the value of such lags. The lags between an innovation being discovered and its adoption by the entirety of the world feels very large, given that living standards in Europe during the 19th century were considerably higher than living standards in much of Africa or India today, but also likely decreasing over time. Conversely, however, as countries benefit from trade with each other an increase in the productive capacity of one country will benefit all others through comparative advantage, and some sectors in developing countries, such as the Indian IT sector, may be able to rapidly absorb productivity improvements abroad. For the purposes of this post, a discount rate of 5% and a lag to reach 30%2 of the world’s population of 10 years, and an infinite lag to reach the remainder, will be conservatively assumed, which is equivalent to a valuation discount factor of about 0.6.
The numbers above imply that global income per capita would be 27.8% higher had the increase in US regulations since 1949 not occurred, which assuming the increase would have been spread evenly across the 30% of the global population that otherwise would have experienced it represents an annual loss of 1.56 billion utils (value of an increase in income of a factor of e) or 78.7 trillion Open Phil dollars (marginal value of a dollar to someone on an income of $50,000), or under a 5% discount rate a loss to infinity of 40.0 billion utils and 1.99 quadrillion Open Phil dollars assuming regulation increases at the same rate to infinity. Assuming that both the benefits and costs of regulation have unitary elasticities with respect to the total quantity of regulation, if native welfare is as valuable as foreign welfare the optimal value of regulation for the United States decreases by about 78% if the current level of regulation is privately optimal3.
This result is rather stark: taken at face value it implies the removal of almost the entirety of the increase in the period covered if foreign and domestic welfare are equally valuable - and renders this regulatory innovation externality of comparable, and soon to be greater, size than the entirety of climate change on a GDP-effect basis, merely from the actions of the United States alone4. It is on another level unsurprising though: any reduction in trend output necessarily causes long-run output over the span of decades to plummet, and the evidence surveyed above indicates that the effects of regulation on trend growth are large indeed.
One potential limitation with this result it that due to cost-benefit analysises usually not being carried out with new regulations, and those that exist often being decades out of date it may be unclear which regulations to abolish, without the perfect rank-order information of their harm that the 78% figure would imply. If we instead have to choose to rip out pages at random from the codebook, we may end up abolishing some of the most beneficial regulations as well as those that are negative once the external effects are included. However, as the above externality is so large in the case where we have no knowledge and are not risk averse the optimal policy is to abolish the entire codebook, bringing a net annual gain relative to the present of 230 million utils or 11.5 trillion OpenPhil dollars. We can reverse the calculations above to calculate the growth difference that makes us indifferent between abolishing the entire codebook, reaching a figure of 0.4%: if regulation reduces GDP growth due to innovation by less than this every year, then in the case of zero knowledge we should not abolish the entire codebook.
How could this result be overturned? If the regulatory innovation elasticity was overestimated, the claim could fail: however it was shown above that it would need to be out by in excess of a factor of 3. Alternatively, the current amount of regulation could be vastly suboptimally low, meaning that the additional of the effect on citizens of foreign countries still implied that roughly the current or a higher level of regulation would be optimal. Lastly, the elasticities of the regulatory benefits and costs could be incorrect, with the result changing if the benefit elasticity is substantially lower or the cost elasticity substantially higher. These will all be explored in more detail in a future post.
The rough fraction of the combined European, Japanese, Chinese, American, Canadian and Australian populations of the world’s total. Using this figure is conservative for reasons explained above.
And privately optimal regulation would need to be 78% higher than today in order for the current level to be globally optimal.
Assuming RCP 8.5 (the 90th percentile of outcomes if no climate action occurred) and no open borders, climate change remains considerably more important from a welfarist perspective due to reducing the GDP per capita of some countries such as India by 92% compared to potential, with correspondingly large reductions in natural log of consumption if individuals cannot move to colder countries further from the equator en masse. This conclusion might not hold once the impact of all other countries (mostly significantly tighter) regulations or the effects of comparative advantage are included.